Part 1 — Building a deep Q-network to play Gridworld — DeepMind’s deep Q-networks
In this article let’s build a Deep Q-network similar to the DeepMind’s Atari agent to play Gridworld problem. We will build virtually the same system the DeepMind did from scratch to understand the Deep Q-network in detail. We will understand the drawbacks of vanilla Deep Q-network and come up with the clever ways to overcome them.
We have seen how to build a simple Deep Reinforcement Learning agent to help us to increase the revenue for a digital marketing campaign in our previous article.
In 2013, deep reinforcement learning was set off when DeepMind built a agent to play Atari game and were able to defeat the then world champion. DeepMind published a paper entitled “Playing Atari with Deep Reinforcement Learning” that outlined their new approach to an old algorithm, which gave them enough performance to play six of seven Atari 2600 games at record levels. The algorithm they used analyzed only the pixel data from the game similar to the human. The old algorithm they used is called Q-learning. DeepMind made significant modifications to the old algorithm to address some of the issues reinforcement learning algorithm suffered then.
In this article we will understand and build a Vanilla Deep Q-learning model and discuss the drawbacks of it. Later we will also see the techniques used by DeepMind to overcome the limitations of the vanilla algorithm.
What is Q-learning?
We sort of implemented a Q-learning algorithm in our last article when we built a neural network to optimize the ad placement problem. The main idea of Q-learning is that your algorithm predicts the value of a state-action pair, and then you compare this prediction to the observed accumulated rewards at some later time and update the parameters of your algorithm, so that next time it will make better predictions. The Q-learning update rule is mentioned below

The above formula tells us that, the updated Q value at time t is the sum of the current Q-value and the expected Q-value in the future provided we play optimally from the current state. The discount factor (from 0 to 0.99) tells us how important is the future reward for us to take the current action
What is GridWorld?
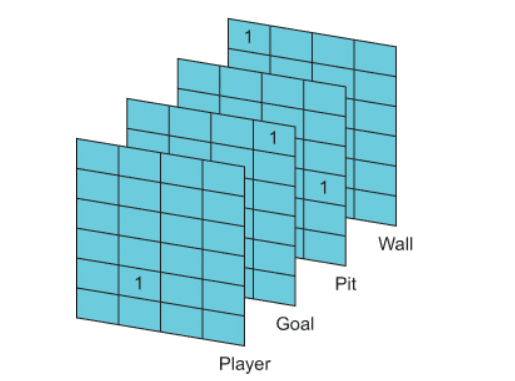
The Gridworld game depicted in figure 2 shows the simple version of Gridworld. The agent (A) must navigate along the shortest path to the goal tile (+) and avoid falling into the pit (–)

The state for a GridWorld is a tensor representing the positions of all the objects on the grid.
Our goal is to train a neural network to play Gridworld from scratch. The agent will have access to what the board looks like. There are four possible actions namely up, down, left and right. Based on the action taken by the agent reward will be received. Reward of -1 is awarded for each move. Any action which leads to a fall in pit or into the wall will receive a reward of -10. Positive reward of +10 is awarded for successfully reaching the goal.
Here’s is the sequence of the steps taken by the agent to play GridWorld
- State of the game
We start the game in some state that we’ll call S(t). The state includes all the information about the game that we have. For our Gridworld example, the game state is represented as a 4 × 4 × 4 tensor. Its is the 4 slice of 4 X 4 grid as shown in fig 3 below

Each grid slice represents the position of an individual object on the board and contains a single 1, with all other elements being 0s. The position of the 1 indicates the position of that slice’s object. As our neural network agent will consume the state as the input vector we will have our input layer with 64 neurons
2. Getting the expected value prediction
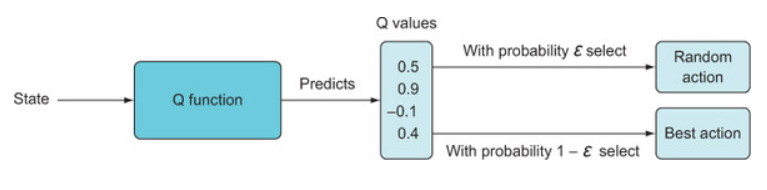
In the vanilla Q-learning algorithm the state S(t) and the candid action is fed to the network and it predicts the expected value which is a single value. In our case we have 4 possible actions and network should predict expected value 4 times with each action as an input. This will only increase the overhead and the processing time of the network. Hence DeepMind came with an idea to make network predict the probability distribution of all the actions . With this change the network has to make prediction only once. But this time the output vector will contain the probability distribution of all the possible actions. In our case the output of the network would be a vector of length 4 . The action corresponding to the max probability can be considered as the best at any particular state. The below image explains the change

3. Choosing the best action
Once we get the prediction of the probability distribution of each state from the network, we need to choose an action to take. For this we can use the epsilon-greedy policy. With epsilon-greedy policy we choose a value of epsilon and with that probability we choose an random action (exploration) ignoring the predicted probability. With probability 1 — epsilon, we will select the action associated with the highest predicted Q value.
Once the action is selected A(t), we will end up in a new state S(t+1) with observed reward R(t+1). The prediction of the expected value we got at S(t) is the predicted Q(S(t),A(t)).We now want to update our network with the actual reward it received for taking the action it recommended
4. Get the reward at (t+1)
Now we run the network at s(t+1) and get the expected value which we call as Q(S(t+1),a) and figure out the action we need to take. To be clear, this is a single value that reflects the highest predicted Q value, given our new state and all possible actions.
5. Update the network
We’ll perform one iteration of training using some loss function, such as mean-squared error, to minimize the difference between the predicted value from our network and the target prediction of

Above steps might be confusing for the first time readers (even I was confused when I was first going through the concepts). Lets start coding and I’m sure that the confusion will be cleared
Let’s code!!!
Creating a GridWorld game
You’ll find two files named GridWorld.py and GridBoard.py in this GIT repository. Please download them and keep them in the same folder where you build your RL agent. These contain some classes to run the game instance. You can create a game instance by the code below
from Gridworld import Gridworld
game = Gridworld(size=4, mode='static')
There are three ways to initialize the board. The first is to initialize it statically, as shown above, so that the objects on the board are initialized at the same predetermined locations. Second, you can set mode=’player’ so that just the player is initialized at a random position on the board. Last, you can initialize it so that all the objects are placed randomly (which is harder for the algorithm to learn) using mode=’random’. We’ll use all three options eventually. More actions on making the moves and checking the rewards can be found in this GIT link
Building a Neural Network as a Q function
Let’s build a neural network as a Q function. We have already discussed the input and output vector size of the neural network. Our input will be a 4X4X4 vector (state vector) and output will be of 4 element vector which is the probability distribution of all the possible actions (up, down, left, right).

Code of the neural network in Pytorch is shown below
import numpy as np
import torch
from Gridworld import Gridworld
import random
from matplotlib import pylab as plt
l1 = 64
l2 = 150
l3 = 100
l4 = 4
model = torch.nn.Sequential(
torch.nn.Linear(l1, l2),
torch.nn.ReLU(),
torch.nn.Linear(l2, l3),
torch.nn.ReLU(),
torch.nn.Linear(l3,l4)
)
loss_fn = torch.nn.MSELoss()
learning_rate = 1e-3
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)
gamma = 0.9
epsilon = 1.0
Once the neural network is ready, we need to create a training loop to train our RL agent and make it learn as per the Q-learning formula given in Fig 1. For this we follow below steps
- Create a for loop for number of epochs
- Initialize the state of the GridWorld
- Create a while loop to monitor the episode of the game
- Run the Q-network forward to get the eval Q value of the current state
- Use greedy epsilon method to choose the action
- Take action as deceided in the previous step to arrive at a new state s` with reward r(t+1)
- Run the Q-network forward at state s` and collect the highest Q value which we call as maxQ
- Our target value for training the network is r(t+1) + γ*maxQA(S(t+1)), where γ (gamma) is a parameter between 0 and 1. If after taking action at the game is over, there is no legitimate s(t+1), so γ*maxQA(S(t+1)) is not valid and we can set it to 0. The target becomes just r(t+1).
- Given that we have four outputs and we only want to update (i.e., train) the output associated with the action we just took, our target output vector is the same as the output vector from the first run, except we change the one output associated with our action to the result we computed using the Q-learning formula.
- Train the model on this one step and repeat steps 2 to 9
Code for the above steps is mentioned below
epochs = 1000
losses = [] 1
for i in range(epochs): 2
game = Gridworld(size=4, mode='static') 3
state_ = game.board.render_np().reshape(1,64) \
+ np.random.rand(1,64)/10.0 4
state1 = torch.from_numpy(state_).float() 5
status = 1 6
while(status == 1): 7
qval = model(state1) 8
qval_ = qval.data.numpy()
if (random.random() < epsilon): 9
action_ = np.random.randint(0,4)
else:
action_ = np.argmax(qval_)
action = action_set[action_] 10
game.makeMove(action) 11
state2_ = game.board.render_np().reshape(1,64) +
np.random.rand(1,64)/10.0
state2 = torch.from_numpy(state2_).float() 12
reward = game.reward()
with torch.no_grad():
newQ = model(state2.reshape(1,64))
maxQ = torch.max(newQ) 13
if reward == -1: 14
Y = reward + (gamma * maxQ)
else:
Y = reward
Y = torch.Tensor([Y]).detach()
X = qval.squeeze()[action_] 15
loss = loss_fn(X, Y)
optimizer.zero_grad()
loss.backward()
losses.append(loss.item())
optimizer.step()
state1 = state2
if reward != -1: 16
status = 0
if epsilon > 0.1: 17
epsilon -= (1/epochs)
1 Creates a list to store loss values so we can plot the trend later
2 The main training loop
3 For each epoch, we start a new game.
4 After we create the game, we extract the state information and add a small amount of noise. This is done to avoid the ‘dead neurons’ which happens with ReLU activation
5 Converts the numpy array into a PyTorch tensor and then into a PyTorch variable
6 Uses the status variable to keep track of whether or not the game is still in progress
7 While this game is still in progress, plays to completion and then starts a new epoch
8 Runs the Q-network forward to get its predicted Q values for all the actions
9 Selects an action using the epsilon-greedy method
10 Translates the numerical action into one of the action characters that our Gridworld game expects
11 After selecting an action using the epsilon-greedy method, takes the action
12 After making a move, gets the new state of the game
13 Finds the maximum Q value predicted from the new state
14 Calculates the target Q value
15 Creates a copy of the qval array and then updates the one element corresponding to the action taken
16 If reward is –1, the game hasn’t been won or lost and is still in progress
17 Decrements the epsilon value each epoch
We also action_set. The GridWorld expects actions to be in alphabets like ‘u’ for up and so on. This dictionary maps the numbers to the corresponding actions as shown below
action_set = {
0: 'u',
1: 'd',
2: 'l',
3: 'r',
}
Training the above network for 1000 epochs gives us amazing results. Once trained we can see the loss decreasing as below

The code to test the model is given below. The test function is same as train except we don’t have loss calculation to back propagate into the model. We just run the model forward to get the predictions and use the action with max value.
def test_model(model, mode='static', display=True):
i = 0
test_game = Gridworld(mode=mode)
state_ = test_game.board.render_np().reshape(1,64) + np.random.rand(1,64)/10.0
state = torch.from_numpy(state_).float()
if display:
print("Initial State:")
print(test_game.display())
status = 1
while(status == 1): 1
qval = model(state)
qval_ = qval.data.numpy()
action_ = np.argmax(qval_) 2
action = action_set[action_]
if display:
print('Move #: %s; Taking action: %s' % (i, action))
test_game.makeMove(action)
state_ = test_game.board.render_np().reshape(1,64) + np.random.rand(1,64)/10.0
state = torch.from_numpy(state_).float()
if display:
print(test_game.display())
reward = test_game.reward()
if reward != -1:
if reward > 0:
status = 2
if display:
print("Game won! Reward: %s" % (reward,))
else:
status = 0
if display:
print("Game LOST. Reward: %s" % (reward,))
i += 1
if (i > 15):
if display:
print("Game lost; too many moves.")
break
win = True if status == 2 else False
return win
Running the above test function with static model will give us a result something like
test_model(model, 'static')
Initial State:
[['+' '-' ' ' 'P']
[' ' 'W' ' ' ' ']
[' ' ' ' ' ' ' ']
[' ' ' ' ' ' ' ']]
Move #: 0; Taking action: d
[['+' '-' ' ' ' ']
[' ' 'W' ' ' 'P']
[' ' ' ' ' ' ' ']
[' ' ' ' ' ' ' ']]
Move #: 1; Taking action: d
[['+' '-' ' ' ' ']
[' ' 'W' ' ' ' ']
[' ' ' ' ' ' 'P']
[' ' ' ' ' ' ' ']]
Move #: 2; Taking action: l
[['+' '-' ' ' ' ']
[' ' 'W' ' ' ' ']
[' ' ' ' 'P' ' ']
[' ' ' ' ' ' ' ']]
Move #: 3; Taking action: l
[['+' '-' ' ' ' ']
[' ' 'W' ' ' ' ']
[' ' 'P' ' ' ' ']
[' ' ' ' ' ' ' ']]
Move #: 4; Taking action: l
[['+' '-' ' ' ' ']
[' ' 'W' ' ' ' ']
['P' ' ' ' ' ' ']
[' ' ' ' ' ' ' ']]
Move #: 5; Taking action: u
[['+' '-' ' ' ' ']
['P' 'W' ' ' ' ']
[' ' ' ' ' ' ' ']
[' ' ' ' ' ' ' ']]
Move #: 6; Taking action: u
[['+' '-' ' ' ' ']
[' ' 'W' ' ' ' ']
[' ' ' ' ' ' ' ']
[' ' ' ' ' ' ' ']]
Reward: 10
We can see that in static state the model performs really good. But the performance is not so good ( infact bad ) in Random state
>>> testModel(model, 'random')
Initial State:
[[' ' '+' ' ' 'P']
[' ' 'W' ' ' ' ']
[' ' ' ' ' ' ' ']
[' ' ' ' '-' ' ']]
Move #: 0; Taking action: d
[[' ' '+' ' ' ' ']
[' ' 'W' ' ' 'P']
[' ' ' ' ' ' ' ']
[' ' ' ' '-' ' ']]
Move #: 1; Taking action: d
[[' ' '+' ' ' ' ']
[' ' 'W' ' ' ' ']
[' ' ' ' ' ' 'P']
[' ' ' ' '-' ' ']]
Move #: 2; Taking action: l
[[' ' '+' ' ' ' ']
[' ' 'W' ' ' ' ']
[' ' ' ' 'P' ' ']
[' ' ' ' '-' ' ']]
Move #: 3; Taking action: l
[[' ' '+' ' ' ' ']
[' ' 'W' ' ' ' ']
[' ' 'P' ' ' ' ']
[' ' ' ' '-' ' ']]
Move #: 4; Taking action: l
[[' ' '+' ' ' ' ']
[' ' 'W' ' ' ' ']
['P' ' ' ' ' ' ']
[' ' ' ' '-' ' ']]
Move #: 5; Taking action: u
[[' ' '+' ' ' ' ']
['P' 'W' ' ' ' ']
[' ' ' ' ' ' ' ']
[' ' ' ' '-' ' ']]
Move #: 6; Taking action: u
[['P' '+' ' ' ' ']
[' ' 'W' ' ' ' ']
[' ' ' ' ' ' ' ']
[' ' ' ' '-' ' ']]
Move #: 7; Taking action: d
[[' ' '+' ' ' ' ']
['P' 'W' ' ' ' ']
[' ' ' ' ' ' ' ']
[' ' ' ' '-' ' ']]
# we omitted the last several moves to save space
Game lost; too many moves.
We see that in Random mode the agent is not able to win the game. Training the model on Random mode is also not so successful and leads to loss plot something like below

What went wrong?
We were able to train our model on a static environment where every time the model saw objects, player and goal in the same position. But when agent was trained on more complicated initialization where environment was randomly initialized everytime a new episode is created, it failed to learn . This is a problem which DeepMind also faced and called it as ‘Catastrophic forgetting’. They came up with a very simple but brilliant idea to overcome this which is called as Experience ‘Replay’.
Let’s understand the problem and the solution in detail in the next part of this article here.
Get the full code used in this article from GIT link
Till now!!
- We started this article understanding what is Q-learning and the formula used to update the Q-learning
- Later we saw GridWorld game and defined its state, actions and rewards.
- Then we came up with a Reinforcement Learning approach to win the game
- We learnt how to import the GridWorld environment and various modes of the environment
- Designed and built a neural network to act as a Q function .
- We trained and tested our RL agent and got very good result in solving static GridWorld. But we failed to solve Random GridWorld.
- We understand what is the problem and promise to solve it in our next article here
Check out the part 2 of the article here:
Part 2 — Building a deep Q-network to play Gridworld — Catastrophic Forgetting and Experience…
Part 1 — Building a deep Q-network to play Gridworld — DeepMind’s deep Q-networks was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
This content was originally published here.